Chap 6. Error Detection and Correction
< Errors >
: transmission(전송)과 reception(수신) 사이에 비트가 변경되면 오류가 발생
– 1 전송 → 0 수신
– 0 전송 → 1 수신
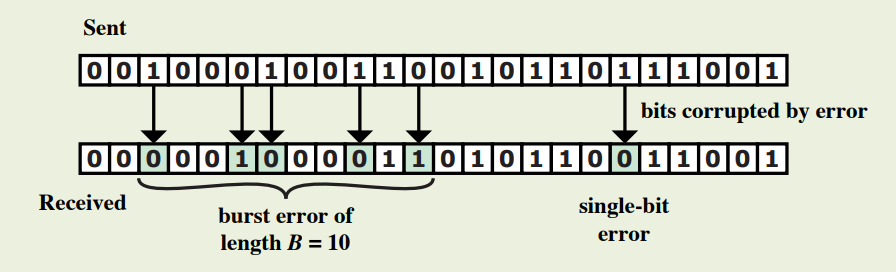
> Single bit errors
: 1 bit를 변경하는 isolated error. 주변 bits에게는 영향 x
: white noise에 의해 발생
> Burst errors
: 첫 번째와 마지막 비트 및 임의의 수의 중간 비트가 오류로 수신되는 연속적인 sequence
: impulse noise, fading in a mobile wireless environment에 의해 발생
: data rates ↑ → error의 효과 ↑
< Error Control >
- Digital transmission systems에 의해 errors 발생
예) Copper wires, BER = 10^-6
예) Optical fiber, BER= 10^-9
예) Wireless transmission, BER = 10^-3
*BER: 수신한 bit에 error가 있을 확률
- Applications의 특정 reliability level 요구 사항
예) Data applications는 error-free transfer가 필요
예) Voice & video applications는 일부 errors 허용 (다시 보내지 x 현재 것으로)
: transmission system이 application의 요구 사항을 충족하지 못할 때 오류 제어가 사용
: Error control을 통해, 오류에도 불구하고 data stream이 일정 수준의 정확도로 전송
< Error Control Approaches >
1. Error detection & ARQ - error 감지
– receiver는 오류를 감지하고 오류가 감지되면 자동 재전송 요청(ARQ)을 전송
– 재전송 요청에는 return channel 필요 o
2. Forward error correction (FEC) - error 수정
– sender는 메시지에 error correction code라고 하는 redundant data(중복 데이터)를 추가
-> 이를 통해 receiver는 sender에 추가 데이터를 요청할 필요 없이 (일부 범위 내에서) 오류를 감지하고 수정
– bandwidth requirements↑ -> return channel 필요x, 데이터 재전송 x
(한번 갈 때 더 보내자!)
– 비용이 많이 들거나 재전송이 불가능한 상황에 적용
예) 위성 및 우주 통신, 오디오/비디오 CD 녹화
< Error Detection >

: 전송된 모든 data blocks (“codewords”)은 패턴을 만족
: 수신된 블록이 패턴 만족 x → 오류
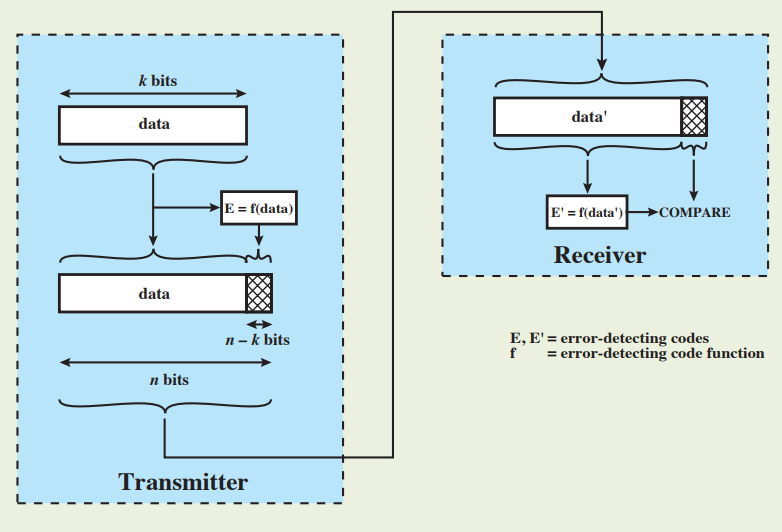
: 보내고자 하는 data에 error detecting code를 붙여 함께 전송
- Redundancy(여분): 전송에 필요한 추가 정보
- Blindspot(사각지대): 채널이 codeword를 다른 codeword로 변환하는 경우
< 종류 >
1) Single Parity Check
2) Two-Dimensional Parity Check
3) Internet Checksum
4) CRC (Cyclic Redundancy Check)
3, 4) 실제 많이 이용!
< Single Parity Check >
Redundancy
: Single parity check code k개의 정보 비트당 1개의 parity bit를 data 끝에 추가
→ Overhead = 1 / (k + 1)
Info Bits: b1, b2, b3, … , bk
Check Bit: [ b(k+1) = b1+ b2+ b3+ … + bk ] modulo 2 // 1이 짝수개면 0, 홀수개면 1
Codeword: b1, b2, b3, …, bk, bk+1
: ASCII 코드에 사용
: error가 발생하는 bit의 수가 짝수개인 경우, error detecting이 불가능
: error가 발생하는 bit의 수가 홀수개인 경우, error detecting이 가능
→ 50% 확률로 감지
- Even parity(0): 1의 개수를 even하게 만드는 parity bit
- Odd parity(1): 1의 개수를 odd하게 만드는 parity bit
< Example >
Information (7 bits): ( 0, 1, 0, 1, 1, 0, 0 )
Parity Bit: b8 = 0 + 1 + 0 + 1 +1 + 0 = 1
Codeword (8 bits): ( 0, 1, 0, 1, 1, 0, 0, 1 )
- error가 3번째 bit에서 발생
: ( 0, 1, 1, 1, 1, 0, 0, 1 ) → 1이 4개 → parity bit=1 이므로 오류 감지o → 어디인지 모름
- error가 3, 5번째 bit에서 발생
: ( 0, 1, 1, 1, 0, 0, 0, 1 ) → 1이 3개 → parity bit = 1 이므로 오류 감지 x

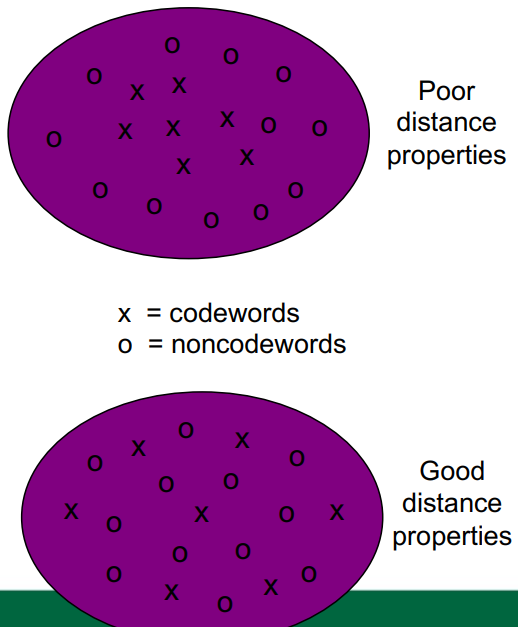
< 좋은 코드의 조건 >
- codewords가 서로 가까이 있으면 detection failures 발생
- codeword 간의 분리를 최대화 → 채널이 하나의 유효한 codeword를 다른 codeword로 변환할 가능성을 최소화
- 정보를 추가하여 멀리 배치 (= 추가비트 실음)
< bit error가 random일 때 >
1) 감지할 수 있는 error pattern이 발생할 확률
bit errors - random, 독립적, 확률 p
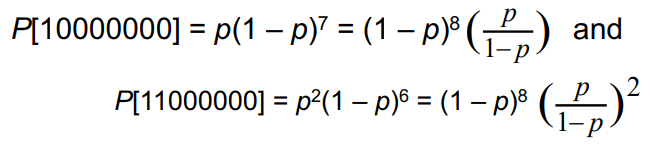
: p < 0.5 → p / (1 – p) < 1
: 오류가 1개인 패턴 > 오류가 2개인 패턴
2) 감지할 수 없는 error pattern이 발생할 확률
P[error 감지 실패]
= P[검출할 수 없는 error pattern]
= P[error가 발생하는 bit의 수가 짝수개인 경우]
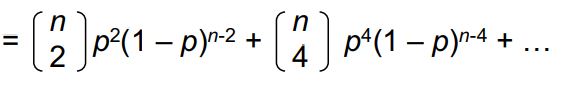
예) n = 32, p = 10^-3
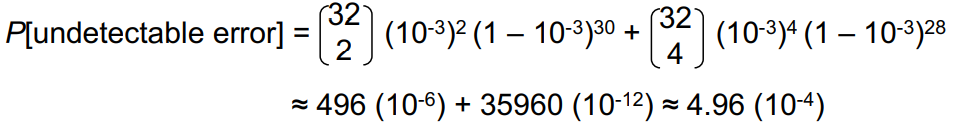
→ 1/2000의 확률로 error pattern 검출 불가

< Two-Dimensional Parity Check >
: 범위를 개선하기 위한 더 많은 parity bit
: 정보를 columns(열)로 정렬
: 각 열에 single parity bit 추가
: 최종 "parity" 열 추가
: 초기 error control systems에 사용
: 행과 열의 변화가 쌍을 이루게 되면, error detecting이 불가능
: require too many check bits

→ overhead = 10/30 = 1/3
< Internet Checksum >
: 송신 측의 checksum 계산 결과에 1의 보수를 취한 형태를 data 끝에 추가하고, 수신 측의 checksum verification 수행
: 몇몇 Internet protocols (IP, TCP, UDP)는 check bits를 사용하여 IP header, TCP/UDP용 header 및 data의 errors 감지
: header contents에 대한 checksum이 계산되고 special field에 포함
: 모든 routers에서 checksum 재계산 → 소프트웨어에서 쉽게 구현할 수 있도록 알고리즘이 선택
: Let header consist of L, 16-bit words, b0, b1, b2, ..., bL-1
→ algorithm이 16-bit checksum bL을 추가
: error 없는 전송을 위해 transport layer로 전달
: 상대 transport layer에서 error를 판단할 수 있도록 error check를 위한 정보를 data에 추가
CRC보다 성능은 낮지만 overhead가 없도록 하는 간단한 방법
< 계산법 >
1. Treating each 16-bit word as an integer, find x = b0 + b1 + b2+ ...+ bL-1 modulo 2^16 - 1
2. The checksum is then given by: bL = -x modulo 2^16 - 1
3. Thus, the headers must satisfy the following pattern: 0 = b0 + b1 + b2+ ...+ bL-1 + bL modulo 2^16-1
4. The checksum calculation is carried out in software using one’s complement arithmetic
< Example >
b0 = 1100, b1 = 1010, b2 = ?
| Use Modulo Arithmetic | Use Binary Arithmetic |
| Assume 4-bit words - Use mod 2^4-1 arithmetic - b0 = 1100 = 12 - b1 = 1010 = 10 - b0 + b1 = 12 + 10 = 22 → 22 mod 15 = 7 mod 15 → 7 → b2 = -7 = 8 mod 15 - Therefore b2 = 1000 |
- Note 16 = 1, (mod 15) - So: 10000 = 0001 mod 15 - leading bit wraps around b0 + b1 = 1100 + 1010 = 10110 = 0110 + 1 (wraps around) = 0111 Take 1s complement b2 = - 0111 = 1000 |
< Example >
b0 = 1110, b1 = 1010, b2 = 0101, b3 = 0011, b4 = ?
| Use Modulo Arithmetic | Use Binary Arithmetic |
| Assume 4-bit words - Use mod 2^4-1 arithmetic - b0 = 1110 = 14 - b1 = 1010 = 10 - b2 = 0101 = 5 - b3 = 0011 = 3 - b0 + b1 +b2 + b3 = 14 + 10 + 5 + 3 = 32 → 32 mod 15 = 2 mod 15 → 2 → b2 = -2 = 13 mod 15 - Therefore b2 = 1101 |
- Note 16 = 1, (mod 15) - So: 10000 = 0001 mod 15 - leading bit wraps around b0 + b1 + b2 + b3 = 11000 + 1000 = 1000 + 1 (wraps around) + 1000 = 1001 + 1000 = 10001 = 0001 + 1 (wraps around) = 0010 Take 1s complement b2 = - 0010 = 1101 |
< Polynomial Codes - Cyclic Redundancy Check (CRC) >
: vectors x, polynomials o
: checksums x, polynomial arithmetic o
: Shift-Register Circuits를 이용하여 구현
: 대부분의 데이터 통신 표준은 오류 감지를 위해 polynomial codes를 사용
: error-correction 방법의 기초
> D: data bits (binary number)
> G: bit pattern (generator), of r+1 bits
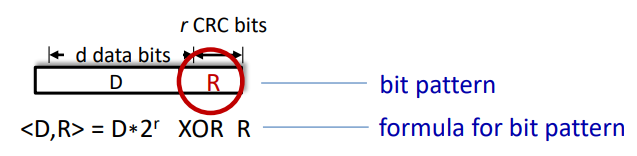
: choose r CRC bits, R, such that exactly divisible by G (mod 2)
: receiver knows G, divides by G
: 나머지가 0이 아니면: error detected
: r+1 bits 미만의 모든 burst errors 감지 가능
: 실제로 널리 사용
예) Ethernet, 802.11 WiFi
< 계산법 >
보내고자 하는 data를 송,수신측이 모두 알고 있는 Divisor로 나눈다 (XOR 연산)
divisor의 bit 수-1 (G-1)만큼 보내고자 하는 data를 shifting (0을 붙여줌)
나머지인 Remainder를 보내고자 하는 data 뒤에 붙여줌
수신측에서 modulo 연산 시, 나머지가 0이 되지 않으면 무조건 error로 감지
1) D*2^r XOR R = nG
2) D*2^r = nG XOR R
3) R = D*2^r XOR nG
D*2^r이 G로 나누어떨어지면
→ R = remainder [ D*2^r / G ]
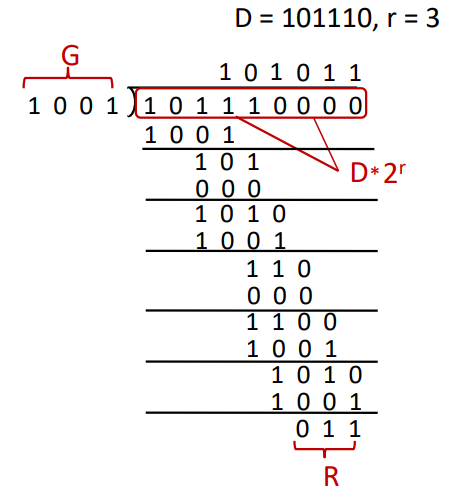
< Example >
generator code: ( 1, 0, 0, 1 ) (g(x) = x^3+1) → CRC bits = 4 - 1 = 3
bit stream: ( 1, 0, 1, 1, 1, 0 )
CRC bits = ?, Codeword = ?
r = 3, D*2^r = 101110000
→ R = 011
→ Codeword = 101110011
< Example >
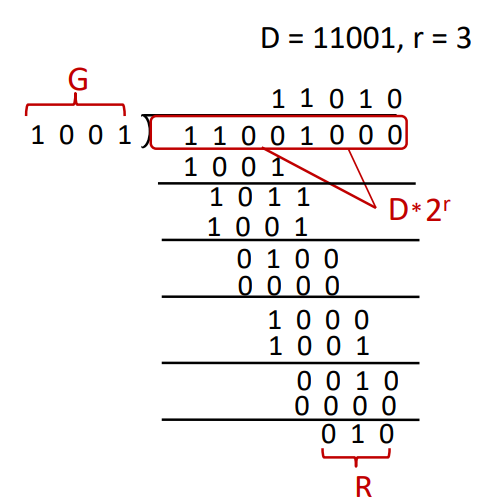
generator code: ( 1, 0, 0, 1 ) (g(x) = x^3+1) → CRC bits = 4 - 1 = 3
bit stream: ( 1, 1, 0, 0, 1 )
CRC bits = ?, codeword = ?
r = 3, D*2^r = 11001000
→ R = 010
→ codeword = 11001010
확인: 11001010 / 1001 = 0
b) randomly choose 1 bit and flip it. Can the error be detectable?
b(x) / g(x) == 0 → no error detected
c) randomly choose 2 bit and flip it. Can the error be detectable?
< Shift-Register circuit of CRC >
: 디지털회로 에서 선형 방식으로 설치된 process register의 집합
: 회로가 활성화되었을 때 데이터를 줄 아래로 이동시키는 것과 같은 방법으로 입출력을 서로 연결

< Example >
generator code: ( 1, 0, 0, 1 ) (g(x) = x^3+1) → CRC bits = 4 - 1 = 3
bit stream: ( 1, 1, 0, 0, 1 )
CRC bits = ?, codeword = ?
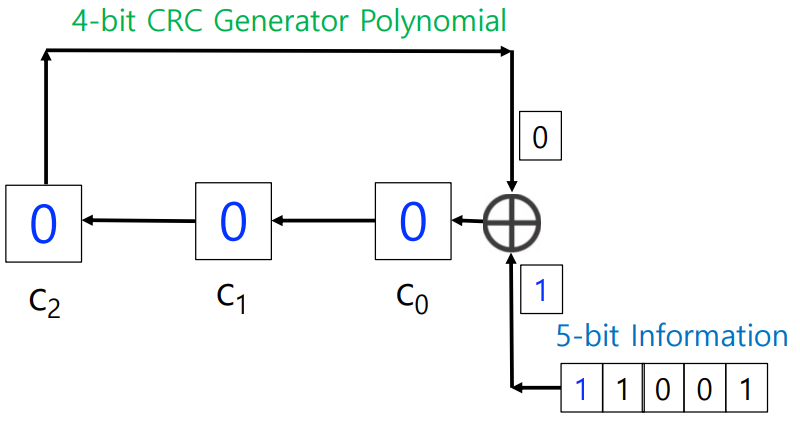
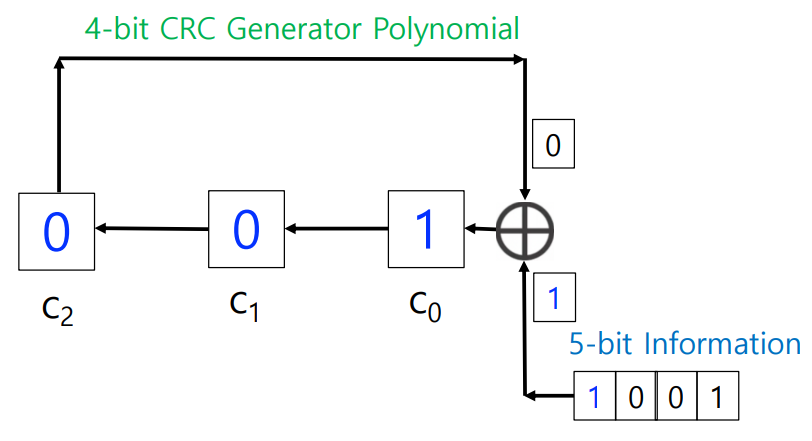
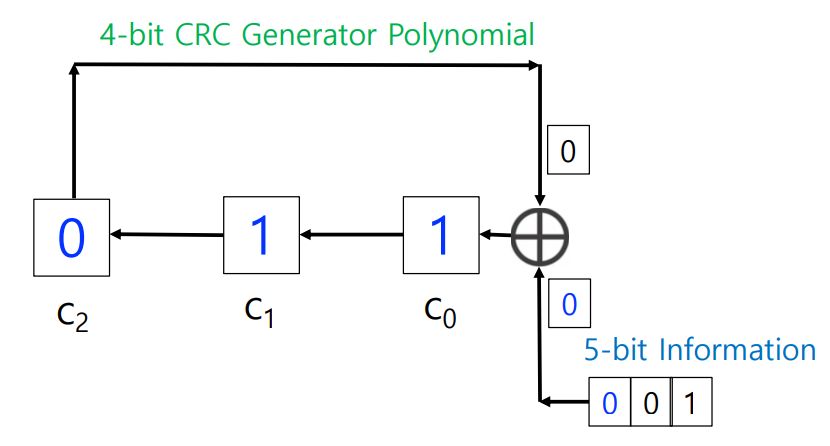
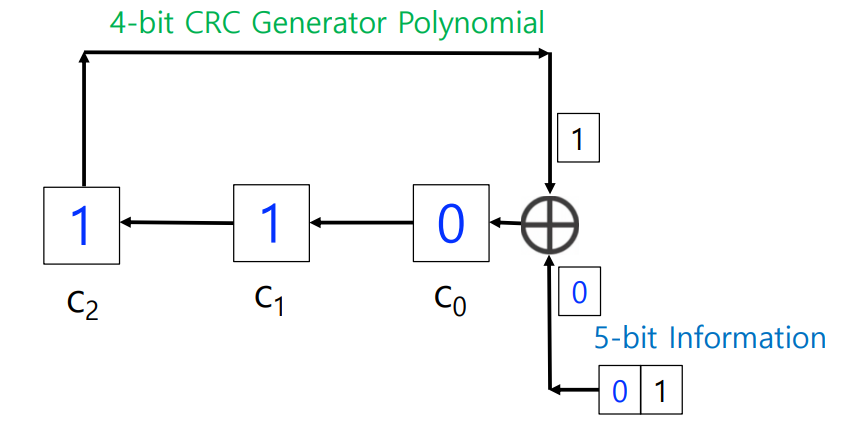
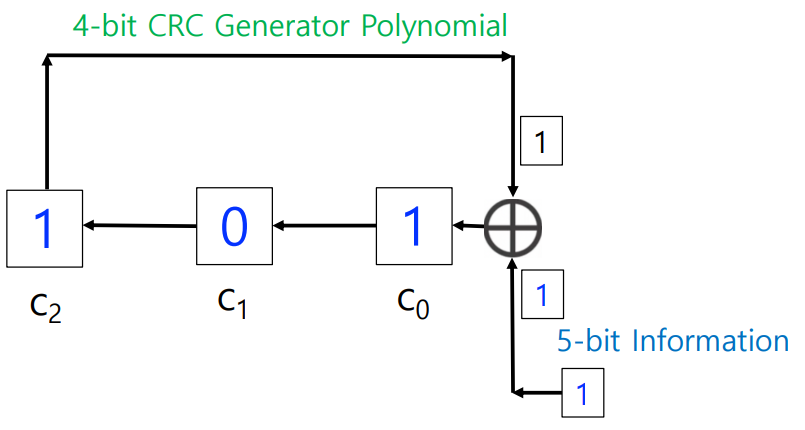
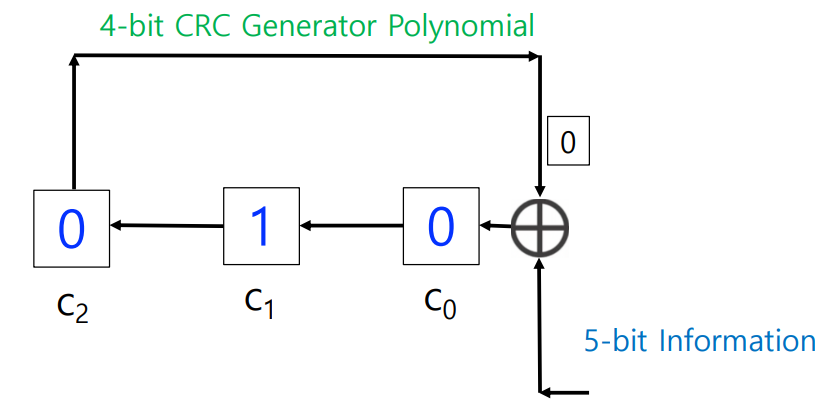
→ R = 010
→ codeword = 11001010
< Binary Polynomial Arithmetic >
- Binary vectors map -> polynomials:
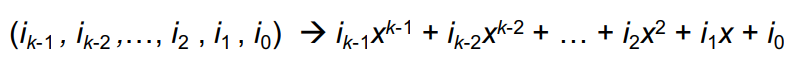
| i6 | i5 | i4 | i3 | i2 | i1 | i0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| x^6 | 0 * x^5 | 0 * x^4 | x^3 | 0 * x^2 | x | 1 |
→ x^6 + x^3 + x + 1
> Addition:
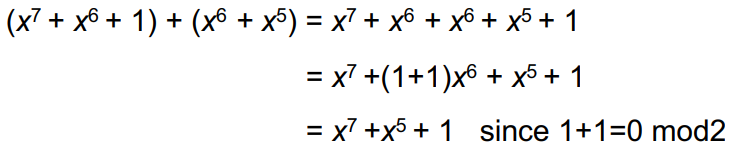
( 1 1 0 0 0 0 0 1 )
+ ( 0 1 1 0 0 0 0 0 )
_______________
1 0 1 0 0 0 0 1
> Multiplication:
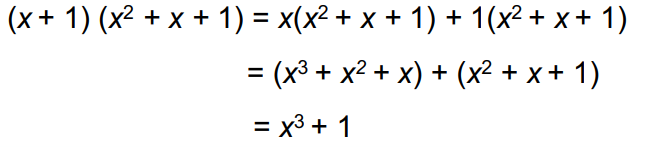
( 1 1 1 0 )
+ ( 0 1 1 1 )
__________
1 0 0 1
> Division:
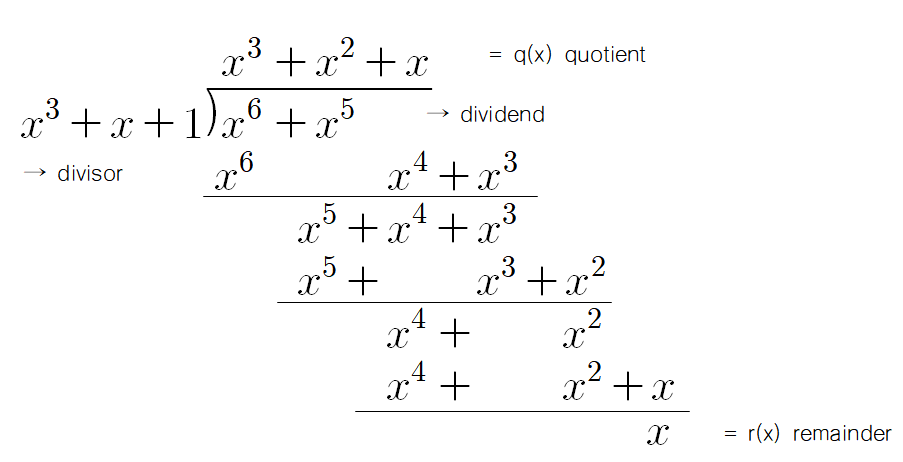
< Polynomial Coding >
1. (n-k)차 다항식 Generator polynomial g(x)
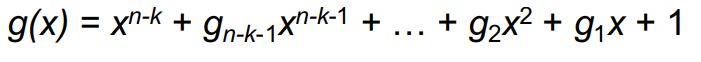
2. k information bits는 (k–1)차의 다항식을 정의
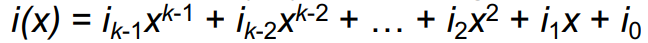
3. (n–k–1)차 다항식의 나머지 찾기
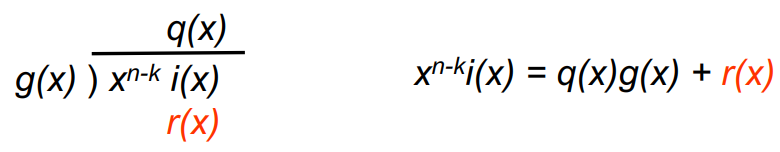
4. (n-1)차 다항식의 codeword:
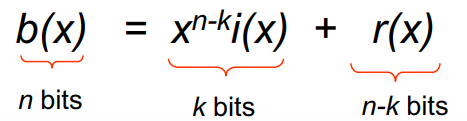
< Example >
k = 4, n = 7, n - k = 3, Transmitted codeword = ?
Generator polynomial: g(x)= x^3 + x + 1 // ( 1, 0, 1, 1 ) → 4bit → CRC는 3bit
Information: (1,1,0,0) → i(x) = x^3 + x^2
Encoding: x^3i(x) = x^6 + x^5
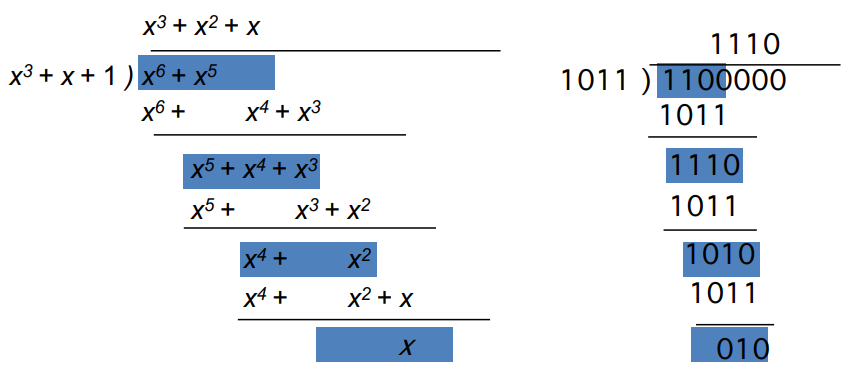
Transmitted codeword
= b(x)
= x^(n-k)i(x) + r(x)
= x^3(x^3 + x^2) + x = x^6 + x^5 + x
→ b = ( 1, 1, 0, 0, 0, 1, 0 )
< Polynomial Coding의 패턴 >
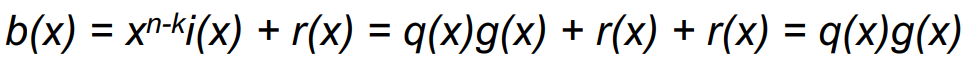
: 모든 codewords는 g(x)의 배수
: receivers는 수신된 n-tuple을 g(x)로 나누고 나머지가 0인지 확인
: 나머지가 0이 아닌 경우 - 수신된 n-tuple은 codeword x
< Standard Generator Polynomials >

교재는 Data and Computer Communications를 참고하였고, 자료는 이화여자대학교 이형준 교수님의 정보통신공학 강의에서 가져온 것입니다.
'Study > 정보통신공학' 카테고리의 다른 글
| [Week 9-1] High Level Data Link Control (HDLC) (0) | 2023.04.28 |
|---|---|
| [Week 7-1, 7-2] Data Link Control Protocols (0) | 2023.04.14 |
| [Week 5-2] Data encoding (Digital Data → Analog Signal, Analog Data → Digital Signal) (1) | 2023.04.13 |
| [Week 5-1] Data Encoding (Digital data → Digital signal) (0) | 2023.04.13 |
| [Week 4-2] Transmission Media - Wire, Wireless (1) | 2023.04.12 |